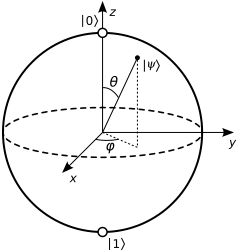
¿Cómo pensar en la puerta Z en una esfera Bloch?

10

Estoy confundido acerca de cómo entender el $Z$ puerta en una esfera de Bloch.

Considerando la matriz $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ es entendible que $Z|0\rangle = |0\rangle$ y $Z|1\rangle = -|1\rangle$ .

Aquí se explica que $Z$ la puerta es $\pi$ rotación alrededor del $Z$ eje. Entonces, ¿cómo debo entender? $Z|1\rangle = -|1\rangle$ ? Ya que $|1\rangle$ es el polo sur, creo que es natural pensar que $\pi$ rotación alrededor del $Z$ axis no hace nada.

quantum-gate bloch-sphere Bick
fuente

7

La forma de pensar sobre la esfera de Bloch es en términos de la matriz de densidad para el estado. $Z$ actuando sobre cualquiera $|0\rangle\langle 0|$ o $|1\rangle\langle 1|$ no hace nada, como es cierto para cualquier matriz de densidad diagonal. Para ver el efecto de la rotación, debe observar cómo cambia cualquier matriz de densidad no diagonal $Z$ , como $|+\rangle\langle +|$ .

DaftWullie
fuente

7

$|1\rangle$ y $-|1\rangle$ se asignan al mismo punto en la esfera de Bloch porque son iguales a la fase global . Algebraicamente: $|1\rangle \equiv -|1\rangle$ dónde $\equiv$ significa "igual a la fase global". Lo que significa que hay algunos $\theta$ tal que $-|1\rangle = e^{i \theta} |1\rangle$ .

Lo que te confunde es eso, a pesar de que $|0\rangle \equiv Z |0\rangle$ y $|1\rangle \equiv Z |1\rangle$ , esto no es cierto para las combinaciones lineales de los dos. Por ejemplo, $Z |+\rangle \not\equiv Z |+\rangle$ aunque . $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$

Craig Gidney
fuente

2

Según Wikipedia , podemos escribir cualquier estado puro como

| ψ ⟩ = \cos (\frac{θ}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{θ}{2}) | 1 ⟩

$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$

Donde y son los ángulos en la esfera Bloch: $\theta$ $\phi$

Casi cualquier punto de la superficie (es decir, estado puro) tiene una representación única en términos de ángulos, excepto los polos. Al igual que en la Tierra, el Polo Sur no tiene una longitud bien definida (cualquier longitud funciona igual), para el estado cualquier fase significa lo mismo. La "latitud" está aquí , conectemos eso a la ecuación: $|1 \rangle$ $\phi$ $\theta$ $\pi$

| 1 ⟩ = \cos (\frac{π}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{π}{2}) | 1 ⟩ =

$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$

= 0 + e^{i ϕ} | 1 ⟩

$= 0 + e^{i \phi} |1 \rangle$

Si está familiarizado con la identidad de Euler, probablemente reconocerá como una rotación en el plano complejo. En particular, dado que es una rotación para , obtenemos el famoso , llegando finalmente a . $e^{i \phi}$ $Z$ $\phi = \pi$ $e^{i \pi} = -1$ $|1 \rangle = - |1 \rangle$

Norrius
fuente

1

Esto está mal. Escribir es engañoso: estos son estados equivalentes en el sentido de que solo difieren en una fase global, pero esto no significa que los vectores de estado sean los mismos. Obtiene ese resultado porque asume que hay una biyección entre vectores de estado y puntos en la esfera de Bloch, que no es el caso. La biyección se ubica entre los puntos en la esfera de Bloch y los estados descritos como matrices de densidad

| 1 ⟩ = - | 1 ⟩

$|1\rangle=-|1\rangle$

glS

@glS Gracias, el que se deduce de eso parecía sospechoso. ¿Tiene sentido mejorar esa respuesta desde su perspectiva, o está completamente equivocado?

1 = - 1

$1=-1$

Norrius

esa es tu llamada =). Creo que la respuesta correcta es la que da DaftWullie (creo que el autor de la pregunta tuvo una idea errónea similar a la de su respuesta). No veo mucho que decir sobre esta pregunta

glS

¿Cómo pensar en la puerta Z en una esfera Bloch?

Respuestas: