¿Por qué las escuelas de los EE. UU. Y el Reino Unido enseñan diferentes métodos para calcular la desviación estándar?

Según tengo entendido, las escuelas del Reino Unido enseñan que la desviación estándar se encuentra usando:

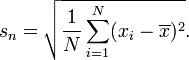
mientras que las escuelas de los Estados Unidos enseñan:

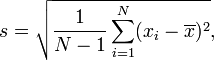
(en un nivel básico de todos modos).

Esto ha causado problemas a varios de mis alumnos en el pasado, ya que buscaron en Internet, pero encontraron la explicación incorrecta.

¿Por qué la diferencia?

Con conjuntos de datos simples que digan 10 valores, ¿qué grado de error habrá si se aplica el método incorrecto (por ejemplo, en un examen)?

La primera fórmula es la desviación estándar de la población y la segunda fórmula es la desviación estándar de la muestra . La segunda fórmula también está relacionada con el estimador imparcial de la varianza; consulte Wikipedia para obtener más detalles.

Supongo que (aquí) en el Reino Unido no hacen la distinción entre muestra y población en la escuela secundaria. Ciertamente no tocan conceptos como estimadores sesgados.

Debido a que nadie ha respondido la pregunta final, es decir, para cuantificar las diferencias entre las dos fórmulas, cuidemos eso.

Por muchas razones, es apropiado comparar las desviaciones estándar en términos de sus proporciones lugar de sus diferencias. La relación es

$|\binom{1/2}{2}N^{-2}|$$1 / (8 N^2)$$N$$2$ o mayor.

$N$$5$$N$$10$SD, como cuando se comparan los diferenciales de dos conjuntos de datos. (Cuando los conjuntos de datos son equinumerosos, las discrepancias desaparecen por completo y ambas fórmulas conducen a conclusiones idénticas). Posiblemente, estas son las formas de razonamiento que estamos tratando de enseñar a los estudiantes principiantes, por lo que si los estudiantes se preocupan sobre qué fórmula usar, eso podría tomarse como una señal de que el texto o la clase no logran enfatizar lo que es realmente importante.

$N$$t$$z$$s$$s_n$

Esta es la corrección de Bessel . La versión estadounidense muestra la fórmula para la desviación estándar de la muestra , donde la versión del Reino Unido anterior es la desviación estándar de la muestra .

No estoy seguro de que esto sea un asunto puramente estadounidense contra británico. El resto de esta página está extraído de un faq que escribí. ( Http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 ).

Cómo calcular la SD con n-1 en el denominador

1. Calcule el cuadrado de la diferencia entre cada valor y la media muestral.

2. Suma esos valores.

3. Divide la suma por n-1. El resultado se llama varianza.

4. Toma la raíz cuadrada para obtener la desviación estándar.

¿Por qué n-1?

¿Por qué dividir por n-1 en lugar de n cuando se calcula una desviación estándar? En el paso 1, calcula la diferencia entre cada valor y la media de esos valores. No sabes la verdadera media de la población; todo lo que sabes es la media de tu muestra. Excepto en los casos excepcionales en los que la media de la muestra es igual a la media de la población, los datos estarán más cerca de la media de la muestra que de la media de la población real. Entonces, el valor que calcula en el paso 2 probablemente será un poco más pequeño (y no puede ser más grande) de lo que sería si usara la media real de la población en el paso 1. Para compensar esto, divida entre n-1 que nv Esto se llama corrección de Bessel.

¿Pero por qué n-1? Si conociera la media de la muestra y todos los valores menos uno, podría calcular cuál debe ser ese último valor. Los estadísticos dicen que hay n-1 grados de libertad.

¿Cuándo debe calcularse la SD con un denominador de n en lugar de n-1?

Los libros de estadísticas a menudo muestran dos ecuaciones para calcular la SD, una con n, y la otra con n-1, en el denominador. Algunas calculadoras tienen dos botones.

La ecuación n-1 se usa en la situación común en la que está analizando una muestra de datos y desea sacar conclusiones más generales. La SD calculada de esta manera (con n-1 en el denominador) es su mejor estimación del valor de la SD en la población general.

Si simplemente desea cuantificar la variación en un conjunto particular de datos, y no planea extrapolar para sacar conclusiones más amplias, puede calcular la SD usando n en el denominador. La SD resultante es la SD de esos valores particulares. No tiene sentido calcular el SD de esta manera si desea estimar el SD de la población de la que se extrajeron esos puntos. Solo tiene sentido usar n en el denominador cuando no hay muestreo de una población, no hay deseo de sacar conclusiones generales.

El objetivo de la ciencia es casi siempre generalizar, por lo que no debe usarse la ecuación con n en el denominador. El único ejemplo que puedo pensar sobre dónde podría tener sentido es cuantificar la variación entre los puntajes de los exámenes. Pero mucho mejor sería mostrar un diagrama de dispersión de cada puntaje, o un histograma de distribución de frecuencia.

Dado que N es el número de puntos en el conjunto de datos, se podría argumentar que al calcular la media se ha reducido en uno el grado de libertad en el conjunto de datos (ya que se introdujo una dependencia en el conjunto de datos), por lo que se debe usar N -1 al estimar la desviación estándar de un conjunto de datos para el cual había que estimar la media antes.