Esta pregunta surge de mi confusión real sobre cómo decidir si un modelo logístico es lo suficientemente bueno. Tengo modelos que usan el estado de pares proyecto individual dos años después de que se forman como una variable dependiente. El resultado es exitoso (1) o no (0). Tengo variables independientes medidas en el momento de la formación de los pares. Mi objetivo es probar si una variable, que supuse que influiría en el éxito de los pares, tiene un efecto sobre ese éxito, controlando otras posibles influencias. En los modelos, la variable de interés es significativa.
Los modelos se estimaron utilizando la glm()función en R. Para evaluar la calidad de los modelos, he hecho algunas cosas: glm()le da el residual deviance, el AICy el BICpor defecto. Además, calculé la tasa de error del modelo y tracé los residuos agrupados.
- El modelo completo tiene una desviación residual, AIC y BIC más pequeña que los otros modelos que he estimado (y que están anidados en el modelo completo), lo que me lleva a pensar que este modelo es "mejor" que los otros.
- La tasa de error del modelo es bastante baja, en mi humilde opinión (como en Gelman y Hill, 2007, pp.99 ):
error.rate <- mean((predicted>0.5 & y==0) | (predicted<0.5 & y==1)alrededor del 20%.
Hasta aquí todo bien. Pero cuando trazo el residuo binned (nuevamente siguiendo el consejo de Gelman y Hill), una gran parte de los contenedores quedan fuera del IC del 95%:
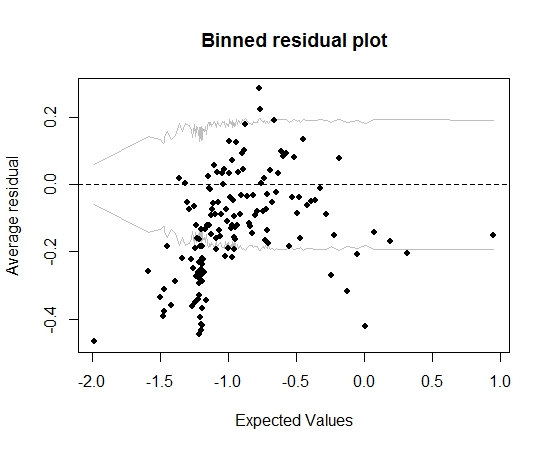
Esa trama me lleva a pensar que hay algo completamente incorrecto en el modelo. ¿Debería eso llevarme a tirar la modelo? ¿Debo reconocer que el modelo es imperfecto pero mantenerlo e interpretar el efecto de la variable de interés? He jugado con variables excluyentes a su vez, y también alguna transformación, sin mejorar realmente el gráfico de residuos agrupados.
Editar:
- Por el momento, el modelo tiene una docena de predictores y 5 efectos de interacción.
- Las parejas son "relativamente" independientes entre sí en el sentido de que todas se forman durante un corto período de tiempo (pero no hablando estrictamente, todo simultáneamente) y hay muchos proyectos (13k) y muchas personas (19k ), por lo que una proporción justa de proyectos solo se unen por un individuo (hay alrededor de 20000 pares).
fuente

Respuestas:
La precisión de clasificación (tasa de error) es una regla de puntuación incorrecta (optimizada por un modelo falso), arbitraria, discontinua y fácil de manipular. No es necesario en este contexto.
No mencionaste cuántos predictores había. En lugar de evaluar el ajuste del modelo, estaría tentado a hacer que el modelo se ajuste. Un enfoque de compromiso es asumir que las interacciones no son importantes y permitir que los predictores continuos sean no lineales utilizando splines de regresión. Trazar las relaciones estimadas. El
rmspaquete en R hace que todo esto sea relativamente fácil. Ver http://biostat.mc.vanderbilt.edu/rms para más información.Puede elaborar sobre "pares" y si sus observaciones son independientes.
fuente
fuente