¿Cómo haría para generar una lista de todas las permutaciones posibles de una cadena entre los caracteres x e y de longitud, que contiene una lista variable de caracteres?
Cualquier idioma funcionaría, pero debería ser portátil.
string
language-agnostic
cross-platform
UnkwnTech
fuente
fuente

Respuestas:
Hay varias formas de hacer esto. Los métodos comunes usan recursividad, memorización o programación dinámica. La idea básica es que produzca una lista de todas las cadenas de longitud 1, luego, en cada iteración, para todas las cadenas producidas en la última iteración, agregue esa cadena concatenada con cada carácter en la cadena individualmente. (el índice variable en el código a continuación realiza un seguimiento del inicio de la última y la próxima iteración)
Algunos pseudocódigo:
entonces deberá eliminar todas las cadenas de menos de x de longitud, serán las primeras entradas (x-1) * len (originalString) en la lista.
fuente
Es mejor usar retroceder
fuente
Tendrás muchas cuerdas, eso seguro ...
Donde x e y es cómo los define yr es el número de caracteres que estamos seleccionando, si lo entiendo correctamente. Definitivamente, debe generarlos según sea necesario y no ponerse descuidado y decir, generar un conjunto de potencia y luego filtrar la longitud de las cadenas.
Lo siguiente definitivamente no es la mejor manera de generarlos, pero es interesante, no obstante.
Knuth (volumen 4, fascículo 2, 7.2.1.3) nos dice que (s, t) combinación es equivalente a s + 1 cosas tomadas t a la vez con repetición - una combinación (s, t) es notación utilizada por Knuth que es igual a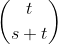 . Podemos resolver esto generando primero cada combinación (s, t) en forma binaria (entonces, de longitud (s + t)) y contando el número de 0 a la izquierda de cada 1.
. Podemos resolver esto generando primero cada combinación (s, t) en forma binaria (entonces, de longitud (s + t)) y contando el número de 0 a la izquierda de cada 1.
10001000011101 -> se convierte en la permutación: {0, 3, 4, 4, 4, 1}
fuente
Solución no recursiva según Knuth, ejemplo de Python:
fuente
"54321"solo se muestra UNA cadena (en sí).nextPermutation()tiene estado: solo se necesita la entrada para permutar y los índices no se mantienen de iteración a iteración. Puede hacerlo asumiendo que la entrada inicial se ordenó y encontrando índices (k0yl0) en sí mismos, en función del lugar donde se mantiene el orden. Ordenar una entrada como "54321" -> "12345" permitiría a este algoritmo encontrar todas las permutaciones esperadas. Pero dado que hace una buena cantidad de trabajo extra para reencontrar esos índices para cada permutación que genera, existen formas más eficientes de hacerlo de manera no recursiva.Puede mirar " Enumerar eficientemente los subconjuntos de un conjunto ", que describe un algoritmo para hacer parte de lo que desea: generar rápidamente todos los subconjuntos de N caracteres de longitud x a y. Contiene una implementación en C.
Para cada subconjunto, aún tendría que generar todas las permutaciones. Por ejemplo, si quisieras 3 caracteres de "abcde", este algoritmo te daría "abc", "abd", "abe" ... pero tendrías que permutar cada uno para obtener "acb", "bac", "bca", etc.
fuente
Algunos códigos Java que funcionan basados en la respuesta de Sarp :
fuente
Aquí hay una solución simple en C #.
Genera solo las permutaciones distintas de una cadena dada.
fuente
Hay muchas buenas respuestas aquí. También sugiero una solución recursiva muy simple en C ++.
Nota : las cadenas con caracteres repetidos no producirán permutaciones únicas.
fuente
Acabo de preparar esto rápidamente en Ruby:
Puede buscar en la API de lenguaje las funciones integradas de tipo de permutación, y puede escribir código más optimizado, pero si los números son tan altos, no estoy seguro de que haya una gran forma de obtener muchos resultados .
De todos modos, la idea detrás del código es comenzar con una cadena de longitud 0, luego realizar un seguimiento de todas las cadenas de longitud Z donde Z es el tamaño actual en la iteración. Luego, revisa cada cadena y agrega cada carácter a cada cadena. Finalmente, al final, elimine los que estaban por debajo del umbral x y devuelva el resultado.
No lo probé con entradas potencialmente sin sentido (lista de caracteres nulos, valores extraños de x e y, etc.).
fuente
Esta es una traducción de la versión Ruby de Mike, a Common Lisp:
Y otra versión, un poco más corta y con más funciones de bucle:
fuente
Aquí hay una palabra simple C # solución recursiva:
Método:
Vocación:
fuente
... y aquí está la versión C:
fuente
Imprime todas las permutaciones sin duplicados
fuente
Solución recursiva en C ++
fuente
En Perl, si desea restringirse al alfabeto en minúsculas, puede hacer esto:
Esto proporciona todas las cadenas posibles entre 1 y 4 caracteres usando caracteres en minúscula. Para mayúscula, el cambio
"a"a"A"y"zzzz"a"ZZZZ".Para el caso mixto, se vuelve mucho más difícil y probablemente no sea factible con uno de los operadores integrados de Perl como ese.
fuente
Respuesta de Ruby que funciona:
fuente
fuente
La siguiente recursividad de Java imprime todas las permutaciones de una cadena dada:
La siguiente es la versión actualizada del método "permut" anterior que hace que n! (n factorial) llamadas menos recursivas en comparación con el método anterior
fuente
No estoy seguro de por qué querrías hacer esto en primer lugar. El conjunto resultante para cualquier valor moderadamente grande de x e y será enorme, y crecerá exponencialmente a medida que x y / o crezcan.
Digamos que su conjunto de caracteres posibles son las 26 letras minúsculas del alfabeto, y le pide a su aplicación que genere todas las permutaciones donde longitud = 5. Suponiendo que no se quede sin memoria obtendrá 11,881,376 (es decir, 26 a la potencia de 5) cuerdas hacia atrás. Aumente esa longitud hasta 6 y obtendrá 308,915,776 cadenas de regreso. Estos números se vuelven dolorosamente grandes, muy rápidamente.
Aquí hay una solución que armé en Java. Deberá proporcionar dos argumentos de tiempo de ejecución (correspondientes a x e y). Que te diviertas.
fuente
Aquí hay una versión no recursiva que se me ocurrió, en JavaScript. No se basa en el anterior no recursivo de Knuth, aunque tiene algunas similitudes en el intercambio de elementos. He verificado su corrección para matrices de entrada de hasta 8 elementos.
Una optimización rápida sería realizar un vuelo previo de la
outmatriz y evitarpush().La idea básica es:
Dada una matriz fuente única, genera un primer conjunto nuevo de matrices que intercambian el primer elemento con cada elemento subsiguiente a su vez, dejando cada uno de los demás elementos sin perturbar. por ejemplo: dado 1234, generar 1234, 2134, 3214, 4231.
Use cada matriz del pase anterior como la semilla para un nuevo pase, pero en lugar de intercambiar el primer elemento, intercambie el segundo elemento con cada elemento posterior. Además, esta vez, no incluya la matriz original en la salida.
Repita el paso 2 hasta que esté listo.
Aquí está el ejemplo de código:
fuente
En rubí:
Es bastante rápido, pero llevará un tiempo =). Por supuesto, puede comenzar en "aaaaaaaa" si las cadenas cortas no son interesantes para usted.
Sin embargo, podría haber malinterpretado la pregunta real: en una de las publicaciones parecía que solo necesitaba una biblioteca de cadenas de fuerza bruta, pero en la pregunta principal parece que necesita permutar una cadena en particular.
Su problema es algo similar a este: http://beust.com/weblog/archives/000491.html (enumere todos los enteros en los que ninguno de los dígitos se repita, lo que resultó en una gran cantidad de idiomas que lo resolvieron, con el ocaml guy usando permutaciones, y algún java guy usando otra solución).
fuente
Necesitaba esto hoy, y aunque las respuestas ya dadas me indicaron en la dirección correcta, no eran exactamente lo que quería.
Aquí hay una implementación usando el método de Heap. La longitud de la matriz debe ser de al menos 3 y, por consideraciones prácticas, no debe ser mayor de 10, dependiendo de lo que desee hacer, paciencia y velocidad de reloj.
Antes de ingresar a su ciclo, inicie
Perm(1 To N)con la primera permutación,Stack(3 To N)con ceros * yLevelcon2**. Al final de la llamada de bucleNextPerm, que devolverá falso cuando hayamos terminado.* VB lo hará por ti.
** Puedes cambiar NextPerm un poco para que esto sea innecesario, pero es más claro de esta manera.
Otros métodos son descritos por varios autores. Knuth describe dos, uno da orden léxico, pero es complejo y lento, el otro se conoce como el método de los cambios simples. Jie Gao y Dianjun Wang también escribieron un artículo interesante.
fuente
Este código en python, cuando se llama con
allowed_charactersset to[0,1]y 4 character max, generaría 2 ^ 4 resultados:['0000', '0001', '0010', '0011', '0100', '0101', '0110', '0111', '1000', '1001', '1010', '1011', '1100', '1101', '1110', '1111']Espero que esto te sea útil. Funciona con cualquier carácter, no solo números
fuente
Aquí hay un enlace que describe cómo imprimir permutaciones de una cadena. http://nipun-linuxtips.blogspot.in/2012/11/print-all-permutations-of-characters-in.html
fuente
Aunque esto no responde a su pregunta exactamente, aquí hay una forma de generar cada permutación de las letras de varias cadenas de la misma longitud: por ejemplo, si sus palabras fueran "café", "joomla" y "moodle", puede esperar resultados como "coodle", "joodee", "joffle", etc.
Básicamente, el número de combinaciones es el (número de palabras) al poder de (número de letras por palabra). Por lo tanto, elija un número aleatorio entre 0 y el número de combinaciones: 1, convierta ese número en base (número de palabras), luego use cada dígito de ese número como el indicador de qué palabra tomar la siguiente letra.
Por ejemplo: en el ejemplo anterior. 3 palabras, 6 letras = 729 combinaciones. Elija un número aleatorio: 465. Convierta a base 3: 122020. Tome la primera letra de la palabra 1, la segunda de la palabra 2, la tercera de la palabra 2, la cuarta de la palabra 0 ... y obtendrá ... "joofle".
Si desea todas las permutaciones, simplemente repita de 0 a 728. Por supuesto, si solo elige un valor aleatorio, una forma mucho
más simple ymenos confusa sería recorrer las letras. Este método le permite evitar la recursividad, si desea todas las permutaciones, ¡además le hace parecer que conoce Maths (tm) !Si el número de combinaciones es excesivo, puede dividirlo en una serie de palabras más pequeñas y concatenarlas al final.
fuente
c # iterativo:
fuente
fuente
Aquí está mi opinión sobre una versión no recursiva
fuente
La solución pitónica:
fuente
Bueno, aquí hay una solución elegante, no recursiva, O (n!):
fuente