Acabo de leer sobre cyclesort a través de una publicación de blog de sortvis.org. Este es probablemente el más oscuro que he escuchado hasta ahora, ya que utiliza matemáticas con las que no estoy familiarizado (detección de ciclos en permutaciones de conjuntos enteros).
¿Cuál es el más oscuro que conoces?
algorithms
sorting
sova
fuente
fuente

Respuestas:
¿Has oído hablar de la paciencia ordenando ? Bueno ahora tienes ...
fuente
Slowsort funciona multiplicando y rindiendo (en lugar de dividir y conquistar). Es interesante porque es probablemente el algoritmo de clasificación menos eficiente que se puede construir (asintóticamente y con la restricción de que dicho algoritmo, aunque sea lento, debe estar trabajando todo el tiempo para obtener un resultado).
Esto lo compensa de bogosort porque, en el mejor de los casos, bogosort es bastante eficiente, es decir, cuando la matriz ya está ordenada. Slowsort no "sufre" de un comportamiento tan favorable. Incluso en su mejor caso, todavía tiene tiempo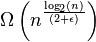 de ejecución para ϵ > 0.
de ejecución para ϵ > 0.
Aquí está su pseudocódigo, adaptado del artículo alemán de Wikipedia :
fuente
No sé si esto cuenta como oscuro, pero uno de los "algoritmos" de clasificación más ridículos es Bogosort . Los enlaces de la página de Bogosort también son divertidos.
Y está esta gema de la sección sobre "cuántica bogo-sort"
Hmmm ... se podría decir que :-).
fuente
Otro "algoritmo" oscuro es la clasificación de diseño inteligente , pero ningún algoritmo es más rápido o tiene menos consumo de memoria :)
fuente
Sleep Sort es bastante novedoso.
fuente
Creo que el tipo de burbuja también sería la respuesta incorrecta en esta situación
:)
fuente
Knuth Volume 3 1 , en la respuesta a uno de los ejercicios, ofrece una implementación de un algoritmo de clasificación sin nombre que es básicamente un antiguo código de golf: el tipo más corto que puede escribir en lenguaje ensamblador MIX. Sin embargo, el código corto tiene el precio tan bajo de la complejidad de O (N 3 ) ...
1 Al menos en las ediciones anteriores. Dadas las modificaciones a MIXAL para la nueva edición, no estoy seguro de si todavía está allí, o incluso tiene el minúsculo sentido en el MIXAL original.
fuente
Para mi clase de estructuras de datos, tuve que (explícitamente) probar la corrección del tipo Stooge . Tiene un tiempo de ejecución de O (n ^ {log 3 / log 1.5}) = O (n ^ 2.7095 ...).
fuente
No sé si es el más oscuro, pero el tipo de espagueti es uno de los mejores en situaciones donde puedes usarlo.
fuente
Uno de los libros originales de Knuth, "Ordenar y buscar", tenía un plegado central que esquematizaba un proceso que clasificaba un archivo de cinta sin disco duro. Creo que usó seis unidades de cinta y mostró explícitamente cuándo se leía cada una hacia adelante, se leía hacia atrás, rebobinando o inactiva. Hoy es un monumento a una tecnología obsoleta.
fuente
Una vez hice una clasificación de burbujas en registros vectoriales en el ensamblador CRAY. La máquina tenía una instrucción de doble cambio, que le permitía cambiar el contenido de un registro vectorial hacia arriba / abajo por una palabra. Ponga el otro punto en dos registros de vectores, luego podría hacer una clasificación de burbuja completa sin tener que hacer otra referencia de memoria hasta que haya terminado. Excepto por la naturaleza N ** 2 del tipo burbuja, fue eficiente.
También una vez tuve que hacer un tipo de coma flotante de un vector de longitud 4 lo más rápido posible para un solo tipo. Lo hice por búsqueda de tabla (el bit de signo de A2-A1 es un bit, el signo de A3-A1 forma otro bit ..., luego buscas el vector de permutación en una tabla. En realidad, fue la solución más rápida que pude encontrar Sin embargo, no funciona bien en arquitecturas modernas, las unidades flotantes y enteras están demasiado separadas.
fuente
Google Code Jam tenía un problema con un algoritmo llamado Gorosort, que creo que inventaron para el problema.
http://code.google.com/codejam/contest/dashboard?c=975485#s=p3
fuente
No recuerdo el nombre, pero básicamente era
fuente
Tipo de concha
Tal vez el algoritmo en sí no sea tan oscuro, pero ¿quién puede nombrar una implementación que realmente se usa en la práctica? ¡Yo puedo!
TIGCC (un compilador basado en GCC para calculadoras gráficas TI-89/92 / V200) usa el ordenamiento Shell para la
qsortimplementación en su biblioteca estándar:Se seleccionó la ordenación de shell a favor de quicksort para mantener bajo el tamaño del código. Aunque su complejidad asintótica es peor, la TI-89 no tiene mucha RAM (190K, menos el tamaño del programa y el tamaño total de las variables no archivadas), por lo que es algo seguro asumir que la cantidad de elementos estar bajo
Se escribió una implementación más rápida después de que me quejé de que era demasiado lenta en un programa que estaba escribiendo. Utiliza mejores tamaños de espacio, junto con optimizaciones de ensamblaje. Se puede encontrar aquí: qsort.c
fuente