Actualmente me estoy preparando para una entrevista, y me recordó una pregunta que me hicieron una vez en una entrevista anterior que era algo como esto:
"Se le pidió que diseñara un software para mostrar continuamente los 10 términos de búsqueda principales en Google. Se le brinda acceso a un feed que proporciona un flujo interminable en tiempo real de términos de búsqueda que se buscan actualmente en Google. Describa qué algoritmo y estructuras de datos que usarías para implementar esto. Debes diseñar dos variaciones:
(i) Muestre los 10 términos de búsqueda principales de todos los tiempos (es decir, desde que comenzó a leer el feed).
(ii) Muestre solo los 10 términos de búsqueda principales del último mes, actualizados cada hora.
Puede utilizar una aproximación para obtener la lista de los 10 principales, pero debe justificar sus elecciones. "
Me equivoqué en esta entrevista y todavía no tengo idea de cómo implementar esto.
La primera parte pide los 10 elementos más frecuentes en una subsecuencia en continuo crecimiento de una lista infinita. Busqué en los algoritmos de selección, pero no pude encontrar ninguna versión en línea para resolver este problema.
La segunda parte utiliza una lista finita, pero debido a la gran cantidad de datos que se están procesando, realmente no puede almacenar todo el mes de términos de búsqueda en la memoria y calcular un histograma cada hora.
El problema se hace más difícil por el hecho de que la lista de los 10 principales se actualiza continuamente, por lo que de alguna manera debe calcular sus 10 principales en una ventana deslizante.
¿Algunas ideas?

what is the most frequent item in the subsequence [2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5] of your sequence?Respuestas:
Bueno, parece una gran cantidad de datos, con un costo quizás prohibitivo para almacenar todas las frecuencias. Cuando la cantidad de datos es tan grande que no podemos esperar almacenarlos todos, ingresamos al dominio de los algoritmos de flujo de datos .
Libro útil en esta área: Muthukrishnan - "Flujos de datos: algoritmos y aplicaciones"
Referencia estrechamente relacionada con el problema en cuestión que seleccioné de lo anterior: Manku, Motwani - "Recuentos de frecuencia aproximados sobre flujos de datos" [pdf]
Por cierto, Motwani, de Stanford, (editar) fue autor del muy importante libro "Randomized Algorithms" .
El capítulo 11 de este libro trata este problema. Editar: Lo siento, mala referencia, ese capítulo en particular tiene un problema diferente. Después de comprobarlo, recomiendo en cambio la sección 5.1.2 del libro de Muthukrishnan , disponible en línea.Je, bonita pregunta de la entrevista.
fuente
Descripción general de la estimación de frecuencia
Existen algunos algoritmos bien conocidos que pueden proporcionar estimaciones de frecuencia para dicho flujo utilizando una cantidad fija de almacenamiento. One is Frequent, de Misra y Gries (1982). De una lista de n elementos, encuentra todos los elementos que ocurren más de n / k veces, usando k - 1 contadores. Ésta es una generalización del algoritmo Mayoría de Boyer y Moore (Fischer-Salzberg, 1982), donde k es 2. LossyCounting de Manku y Motwani (2002) y SpaceSaving de Metwally (2005) algoritmos tienen requisitos de espacio similares, pero pueden proporcionar estimaciones más exactas bajo ciertas condiciones.
Lo importante a recordar es que estos algoritmos solo pueden proporcionar estimaciones de frecuencia. Específicamente, la estimación de Misra-Gries puede subestimar la frecuencia real por (n / k) elementos.
Suponga que tiene un algoritmo que puede identificar positivamente un elemento solo si ocurre más del 50% de las veces. Alimente este algoritmo con un flujo de N elementos distintos y luego agregue otras N - 1 copias de un elemento, x , para un total de 2N - 1 elementos. Si el algoritmo le dice que x excede el 50% del total, debe haber estado en el primer flujo; si no es así, x no estaba en la secuencia inicial. Para que el algoritmo tome esta determinación, debe almacenar el flujo inicial (o algún resumen proporcional a su longitud). Entonces, podemos probarnos a nosotros mismos que el espacio requerido por un algoritmo tan "exacto" sería Ω ( N ).
En cambio, estos algoritmos de frecuencia descritos aquí proporcionan una estimación, identificando cualquier elemento que exceda el umbral, junto con algunos elementos que caen por debajo de él por un cierto margen. Por ejemplo, el algoritmo Mayoría , que utiliza un solo contador, siempre dará un resultado; si algún elemento supera el 50% del flujo, se encontrará. Pero también podría proporcionarle un elemento que aparece solo una vez. No lo sabría sin hacer una segunda pasada sobre los datos (usando, nuevamente, un solo contador, pero buscando solo ese elemento).
El algoritmo frecuente
Aquí hay una descripción simple del algoritmo frecuente de Misra-Gries . Demaine (2002) y otros han optimizado el algoritmo, pero esto le da la esencia.
Especifique la fracción de umbral, 1 / k ; se encontrará cualquier elemento que ocurra más de n / k veces. Cree un mapa vacío (como un árbol rojo-negro); las claves serán términos de búsqueda y los valores serán un contador para ese término.
Tenga en cuenta que puede procesar una cantidad infinita de datos con una cantidad fija de almacenamiento (solo el mapa de tamaño fijo). La cantidad de almacenamiento requerida depende solo del umbral de interés y el tamaño de la secuencia no importa.
Contando búsquedas
En este contexto, tal vez guarde en búfer una hora de búsquedas y realice este proceso con los datos de esa hora. Si puede realizar una segunda pasada sobre el registro de búsqueda de esta hora, puede obtener un recuento exacto de las ocurrencias de los "candidatos" principales identificados en la primera pasada. O tal vez esté bien hacer una sola pasada e informar a todos los candidatos, sabiendo que cualquier elemento que debería estar allí está incluido, y los extras son solo ruido que desaparecerá en la próxima hora.
Cualquier candidato que realmente supere el umbral de interés se almacena como resumen. Guarde un mes de estos resúmenes, desechando los más antiguos cada hora, y tendrá una buena aproximación de los términos de búsqueda más comunes.
fuente
Este es uno de los proyectos de investigación por los que estoy pasando. El requisito es casi exactamente como el tuyo y hemos desarrollado buenos algoritmos para resolver el problema.
La entrada
La entrada es un flujo interminable de palabras o frases en inglés (las llamamos
tokens).La salida
Una aplicación de esta investigación es encontrar el tema candente o las tendencias del tema en Twitter o Facebook. Tenemos un rastreador que rastrea en el sitio web, lo que genera un flujo de palabras, que se alimentará en el sistema. A continuación, el sistema generará las palabras o frases de máxima frecuencia, ya sea en general o históricamente. Imagínense que en las últimas semanas la frase "Copa del Mundo" aparecería muchas veces en Twitter. También lo hace "Paul el pulpo". :)
Cadena en enteros
El sistema tiene un ID entero para cada palabra. Aunque hay casi infinitas palabras posibles en Internet, pero después de acumular un gran conjunto de palabras, la posibilidad de encontrar nuevas palabras es cada vez menor. Ya hemos encontrado 4 millones de palabras diferentes y hemos asignado una identificación única para cada una. Todo este conjunto de datos se puede cargar en la memoria como una tabla hash, consumiendo aproximadamente 300 MB de memoria. (Hemos implementado nuestra propia tabla hash. La implementación de Java requiere una gran sobrecarga de memoria)
Entonces, cada frase puede identificarse como una matriz de números enteros.
Esto es importante, porque ordenar y comparar números enteros es mucho más rápido que en cadenas.
Archivar datos
El sistema mantiene los datos de archivo de cada token. Básicamente son pares de
(Token, Frequency). Sin embargo, la tabla que almacena los datos sería tan grande que tendríamos que particionar la tabla físicamente. Una vez que el esquema de partición se basa en ngramas del token. Si la ficha es una sola palabra, es 1 gramo. Si la ficha es una frase de dos palabras, es 2 gramos. Y esto continúa. Aproximadamente en 4 gramos tenemos mil millones de registros, con un tamaño de tabla de alrededor de 60 GB.Procesamiento de transmisiones entrantes
El sistema absorberá las oraciones entrantes hasta que la memoria se utilice por completo (Sí, necesitamos un MemoryManager). Después de tomar N oraciones y almacenarlas en la memoria, el sistema hace una pausa y comienza a convertir cada oración en palabras y frases. Se cuenta cada ficha (palabra o frase).
Para tokens muy frecuentes, siempre se guardan en la memoria. Para los tokens menos frecuentes, se ordenan en función de los ID (recuerde que traducimos la Cadena en una matriz de números enteros) y se serializan en un archivo de disco.
(Sin embargo, para su problema, dado que solo está contando palabras, puede poner todo el mapa de frecuencia de palabras solo en la memoria. Una estructura de datos cuidadosamente diseñada consumiría solo 300 MB de memoria para 4 millones de palabras diferentes. Alguna sugerencia: use ASCII char para representan cadenas), y esto es muy aceptable.
Mientras tanto, habrá otro proceso que se activará una vez que encuentre cualquier archivo de disco generado por el sistema, luego comenzará a fusionarlo. Dado que el archivo de disco está ordenado, la combinación requeriría un proceso similar como la ordenación por combinación. También hay que tener cuidado con algunos diseños aquí, ya que queremos evitar demasiadas búsquedas de disco aleatorias. La idea es evitar la lectura (proceso de fusión) / escritura (salida del sistema) al mismo tiempo, y dejar que el proceso de fusión se lea desde un disco mientras se escribe en un disco diferente. Esto es similar a implementar un bloqueo.
Fin del día
Al final del día, el sistema tendrá muchos tokens frecuentes con frecuencia almacenados en la memoria y muchos otros tokens menos frecuentes almacenados en varios archivos de disco (y cada archivo está ordenado).
El sistema vacía el mapa en memoria en un archivo de disco (ordénelo). Ahora, el problema se convierte en fusionar un conjunto de archivos de disco ordenados. Usando un proceso similar, obtendríamos un archivo de disco ordenado al final.
Luego, la tarea final es fusionar el archivo de disco ordenado en la base de datos de archivo. Depende del tamaño de la base de datos del archivo, el algoritmo funciona como se muestra a continuación si es lo suficientemente grande:
La intuición es que después de algún tiempo, el número de inserciones será cada vez menor. Cada vez más operaciones se realizarán solo en la actualización. Y esta actualización no será penalizada por index.
Espero que toda esta explicación ayude. :)
fuente
Puede usar una tabla hash combinada con un árbol de búsqueda binaria . Implemente un
<search term, count>diccionario que le diga cuántas veces se ha buscado cada término de búsqueda.Obviamente, iterar toda la tabla hash cada hora para obtener el top 10 es muy malo. Pero estamos hablando de Google, por lo que puede suponer que los diez primeros obtendrán, digamos, más de 10000 visitas (aunque probablemente sea un número mucho mayor). Por lo tanto, cada vez que el recuento de un término de búsqueda supere los 10 000, insértelo en la BST. Luego, cada hora, solo tiene que obtener los primeros 10 del BST, que debería contener relativamente pocas entradas.
Esto resuelve el problema del top 10 de todos los tiempos.
La parte realmente complicada es lidiar con que un término ocupe el lugar de otro en el informe mensual (por ejemplo, "stack overflow" puede tener 50000 visitas durante los últimos dos meses, pero solo 10000 el mes pasado, mientras que "amazon" puede tener 40 000 durante los últimos dos meses, pero 30 000 durante el último mes. Quiere que "amazon" aparezca antes de "stack overflow" en su informe mensual). Para hacer esto, almacenaría, para todos los términos de búsqueda principales (por encima de 10 000 búsquedas de todos los tiempos), una lista de 30 días que le indica cuántas veces se buscó ese término cada día. La lista funcionaría como una cola FIFO: elimina el primer día e inserta uno nuevo cada día (o cada hora, pero luego es posible que deba almacenar más información, lo que significa más memoria / espacio. Si la memoria no es un problema, haga , de lo contrario, busca esa "aproximación"
Parece un buen comienzo. Luego, puede preocuparse por podar los términos que tienen> 10 000 hits pero no han tenido muchos en mucho tiempo y cosas así.
fuente
caso i)
Mantenga una tabla hash para todos los términos de búsqueda, así como una lista ordenada de los diez primeros por separado de la tabla hash. Siempre que se produzca una búsqueda, incremente el elemento apropiado en la tabla hash y verifique si ese elemento ahora debería cambiarse con el décimo elemento en la lista de los diez primeros.
Búsqueda de O (1) para la lista de los diez primeros, y inserción máxima de O (log (n)) en la tabla hash (asumiendo colisiones gestionadas por un árbol binario autoequilibrado).
caso ii) En lugar de mantener una tabla hash enorme y una lista pequeña, mantenemos una tabla hash y una lista ordenada de todos los elementos. Cada vez que se realiza una búsqueda, ese término se incrementa en la tabla hash, y en la lista ordenada se puede verificar el término para ver si debe cambiar con el término posterior. Un árbol binario de autoequilibrio podría funcionar bien para esto, ya que también necesitamos poder consultarlo rápidamente (más sobre esto más adelante).
Además, también mantenemos una lista de 'horas' en forma de lista FIFO (cola). Cada elemento de 'hora' contendría una lista de todas las búsquedas realizadas dentro de esa hora en particular. Entonces, por ejemplo, nuestra lista de horas podría verse así:
Luego, cada hora: si la lista tiene al menos 720 horas de duración (esa es la cantidad de horas en 30 días), observe el primer elemento de la lista y, para cada término de búsqueda, disminuya ese elemento en la tabla hash en la cantidad adecuada . Luego, elimine ese elemento de la primera hora de la lista.
Digamos que estamos en la hora 721 y estamos listos para ver la primera hora en nuestra lista (arriba). Disminuiríamos las cosas gratis en 56 en la tabla hash, las fotos divertidas en 321, etc., y luego eliminaríamos la hora 0 de la lista por completo, ya que nunca tendremos que volver a verla.
La razón por la que mantenemos una lista ordenada de todos los términos que permite consultas rápidas es porque cada hora después, a medida que revisamos los términos de búsqueda de hace 720 horas, debemos asegurarnos de que la lista de los diez primeros permanezca ordenada. Entonces, a medida que disminuimos las 'cosas gratis' en 56 en la tabla hash, por ejemplo, verificaríamos dónde pertenece ahora en la lista. Debido a que es un árbol binario autoequilibrado, todo eso se puede lograr muy bien en un tiempo O (log (n)).
Editar: Sacrificar la precisión por el espacio ...
Puede ser útil implementar también una gran lista en la primera, como en la segunda. Luego, podríamos aplicar la siguiente optimización de espacio en ambos casos: Ejecute un trabajo cron para eliminar todos los elementos de la lista menos los x superiores . Esto mantendría los requisitos de espacio bajos (y como resultado, las consultas en la lista serían más rápidas). Por supuesto, daría como resultado un resultado aproximado, pero esto está permitido. X podría calcularse antes de implementar la aplicación según la memoria disponible y ajustarse dinámicamente si hay más memoria disponible.
fuente
Pensamiento rudo ...
Para los 10 mejores de todos los tiempos
Para los 10 mejores mensuales actualizados cada hora:
Errr ... ¿tiene sentido? No pensé en esto como lo haría en la vida real
Ah, sí, olvidé mencionar que el "copiado / aplanamiento" por hora requerido para las estadísticas mensuales puede reutilizar el mismo código utilizado para los 10 primeros de todos los tiempos, un efecto secundario agradable.
fuente
Solución exacta
Primero, una solución que garantice resultados correctos, pero que requiera mucha memoria (un mapa grande).
Variante "de todos los tiempos"
Mantenga un mapa hash con consultas como claves y sus recuentos como valores. Además, mantenga una lista de las 10 consultas más frecuentes hasta el momento y el recuento del décimo recuento más frecuente (un umbral).
Actualice constantemente el mapa a medida que se lee el flujo de consultas. Cada vez que un recuento exceda el umbral actual, haga lo siguiente: elimine la décima consulta de la lista "10 principales", reemplácela con la consulta que acaba de actualizar y actualice también el umbral.
Variante del "mes pasado"
Mantenga la misma lista de "10 principales" y actualícela de la misma manera que antes. Además, mantenga un mapa similar, pero esta vez almacene vectores de 30 * 24 = 720 recuentos (uno por cada hora) como valores. Cada hora, haga lo siguiente para cada tecla: elimine el contador más antiguo del vector y agregue uno nuevo (inicializado a 0) al final. Quite la clave del mapa si el vector es todo cero. Además, cada hora tienes que calcular la lista "Top 10" desde cero.
Nota: Sí, esta vez almacenamos 720 enteros en lugar de uno, pero hay muchas menos claves (la variante de todos los tiempos tiene una cola realmente larga).
Aproximaciones
Estas aproximaciones no garantizan la solución correcta, pero consumen menos memoria.
fuente
Los 10 términos de búsqueda principales del mes pasado
El uso de una estructura de datos / indexación eficiente en la memoria, como los intentos compactos (de las entradas de wikipedia en los intentos ) define aproximadamente alguna relación entre los requisitos de memoria y n - número de términos.
En caso de que la memoria requerida esté disponible ( suposición 1 ), puede mantener la estadística mensual exacta y agregarla cada mes en la estadística de todos los tiempos.
También hay una suposición aquí que interpreta el "último mes" como una ventana fija. Pero incluso si la ventana mensual se desliza, el procedimiento anterior muestra el principio (el deslizamiento se puede aproximar con ventanas fijas de tamaño determinado).
Esto me recuerda a la base de datos por turnos. con la excepción de que algunas estadísticas se calculan en 'todo el tiempo' (en el sentido de que no se retienen todos los datos; rrd consolida los períodos de tiempo sin tener en cuenta los detalles promediando, sumando o eligiendo valores máximos / mínimos, en una tarea determinada, el detalle que se pierde es la información sobre elementos de baja frecuencia, que pueden introducir errores).
Supuesto 1
Si no podemos mantener estadísticas perfectas durante todo el mes, entonces deberíamos poder encontrar un cierto período P durante el cual deberíamos poder mantener estadísticas perfectas. Por ejemplo, suponiendo que tengamos estadísticas perfectas en algún período de tiempo P, que entra en el mes n veces.
Las estadísticas perfectas definen la función
f(search_term) -> search_term_occurance.Si podemos mantener todas las
ntablas de estadísticas perfectas en la memoria, las estadísticas mensuales deslizantes se pueden calcular de la siguiente manera:ntablas de estadísticas perfectas)Sin embargo, si mantenemos solo los 10 primeros en el nivel agregado (mensual), podremos descartar una gran cantidad de datos de las estadísticas completas del período fijo. Esto ya proporciona un procedimiento de trabajo que tiene requisitos de memoria fijos (asumiendo el límite superior en la tabla de estadísticas perfectas para el período P).
El problema con el procedimiento anterior es que si mantenemos la información solo en los 10 términos principales para una ventana deslizante (de manera similar para todos los tiempos), las estadísticas serán correctas para los términos de búsqueda que alcanzan su punto máximo en un período, pero es posible que no vean el estadísticas de términos de búsqueda que se filtran constantemente a lo largo del tiempo.
Esto se puede compensar manteniendo la información de más de los 10 términos principales, por ejemplo, los 100 términos principales, con la esperanza de que los 10 principales sean correctos.
Creo que un análisis más detallado podría relacionar el número mínimo de ocurrencias necesarias para que una entrada se convierta en parte de las estadísticas (que está relacionado con el error máximo).
(Al decidir qué entradas deben formar parte de las estadísticas, también se puede monitorear y rastrear las tendencias; por ejemplo, si una extrapolación lineal de las ocurrencias en cada período P para cada término le dice que el término será significativo en uno o dos meses ya podría comenzar a rastrearlo. Se aplica un principio similar para eliminar el término de búsqueda del grupo de rastreo).
El peor caso para lo anterior es cuando tiene muchos términos casi con la misma frecuencia y cambian todo el tiempo (por ejemplo, si el seguimiento de solo 100 términos, entonces si los 150 términos principales ocurren con la misma frecuencia, pero los 50 principales son más frecuentes en el primer mes y no sea que a menudo, algún tiempo después, las estadísticas no se mantengan correctamente).
También podría haber otro enfoque que no esté fijo en el tamaño de la memoria (bueno, estrictamente hablando, tampoco lo es el anterior), que definiría la significancia mínima en términos de ocurrencias / período (día, mes, año, todos los tiempos) para el cual mantener el Estadísticas. Esto podría garantizar un error máximo en cada una de las estadísticas durante la agregación (ver round robin nuevamente).
fuente
¿Qué tal una adaptación del "algoritmo de reemplazo de la página del reloj" (también conocido como "segunda oportunidad")? Puedo imaginar que funcionará muy bien si las solicitudes de búsqueda se distribuyen de manera uniforme (eso significa que la mayoría de los términos buscados aparecen regularmente en lugar de 5 millones de veces seguidas y nunca más).
Aquí hay una representación visual del algoritmo: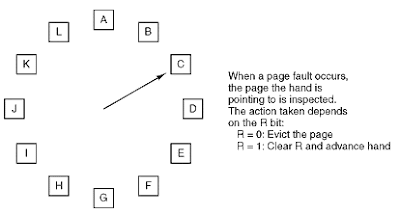
fuente
Almacene el recuento de términos de búsqueda en una tabla hash gigante, donde cada nueva búsqueda hace que un elemento en particular se incremente en uno. Mantenga un registro de los 20 términos de búsqueda principales; cuando se incrementa el elemento en el puesto 11, verifique si necesita intercambiar posiciones con el # 10 * (no es necesario mantener los 10 primeros ordenados; todo lo que le importa es hacer la distinción entre el 10 y el 11).
* Se deben realizar comprobaciones similares para ver si un nuevo término de búsqueda se encuentra en el undécimo lugar, por lo que este algoritmo también incluye otros términos de búsqueda, así que estoy simplificando un poco.
fuente
a veces la mejor respuesta es "No lo sé".
Haré una puñalada más profunda. Mi primer instinto sería introducir los resultados en una Q. Un proceso procesaría continuamente los elementos que entran en la Q. El proceso mantendría un mapa de
término -> contar
cada vez que se procesa un artículo Q, simplemente busca el término de búsqueda e incrementa el recuento.
Al mismo tiempo, mantendría una lista de referencias a las 10 entradas principales del mapa.
Para la entrada que se implementó actualmente, vea si su recuento es mayor que el recuento de la entrada más pequeña en el top 10 (si no está en la lista ya). Si es así, reemplace el más pequeño con la entrada.
Creo que funcionaría. Ninguna operación requiere mucho tiempo. Tendría que encontrar una manera de administrar el tamaño del mapa de conteo. pero eso debería ser suficiente para una respuesta de entrevista.
No esperan una solución, que quieren ver si pueden pensar. No tiene que escribir la solución en ese mismo momento ...
fuente
queue,Qes una letra :).Una forma es que para cada búsqueda, almacene ese término de búsqueda y su marca de tiempo. De esa manera, encontrar los diez primeros para cualquier período de tiempo es simplemente una cuestión de comparar todos los términos de búsqueda dentro del período de tiempo dado.
El algoritmo es simple, pero el inconveniente sería un mayor consumo de memoria y tiempo.
fuente
¿Qué hay de usar un Splay Tree? con 10 nodos? Cada vez que intente acceder a un valor (término de búsqueda) que no esté contenido en el árbol, tire cualquier hoja, inserte el valor y acceda a él.
La idea detrás de esto es la misma que en mi otra respuesta. . Suponiendo que se accede a los términos de búsqueda de manera uniforme / regular, esta solución debería funcionar muy bien.
editar
También se podrían almacenar algunos términos de búsqueda más en el árbol (lo mismo ocurre con la solución que sugiero en mi otra respuesta) para no eliminar un nodo al que se podría acceder muy pronto nuevamente. Cuantos más valores se almacenen en él, mejores serán los resultados.
fuente
No sé si lo entiendo bien o no. Mi solución está usando heap. Debido a los 10 elementos de búsqueda principales, construyo un montón con tamaño 10. Luego actualizo este montón con una nueva búsqueda. Si la frecuencia de una nueva búsqueda es mayor que heap (Max Heap) top, actualícela. Abandona el que tenga la menor frecuencia.
Pero, cómo calcular la frecuencia de la búsqueda específica se contará con otra cosa. Tal vez, como todos dijeron, el algoritmo de flujo de datos ...
fuente
Use cm-sketch para almacenar el recuento de todas las búsquedas desde el comienzo, mantenga un min-montón de tamaño 10 con él para los 10 primeros. Para obtener un resultado mensual, mantenga 30 cm-sketch / hash-table y min-heap con él, cada uno comienza contando y actualizando desde los ultimos 30, 29 .., 1 dia. Como pase de un día, borre el último y utilícelo como el día 1. Lo mismo para el resultado por hora, mantenga 60 hash-table y min-heap y comience a contar los últimos 60, 59, ... 1 minuto. Como pase de un minuto, borre el último y utilícelo como minuto 1.
El resultado mensual es exacto en el rango de 1 día, el resultado por hora es exacto en el rango de 1 min
fuente
El problema no se puede resolver universalmente cuando tiene una cantidad fija de memoria y un flujo 'infinito' (piense muy, muy grande) de tokens.
Una explicación aproximada ...
Para ver por qué, considere un flujo de tokens que tiene un token particular (es decir, una palabra) T cada N tokens en el flujo de entrada.
Además, suponga que la memoria puede contener referencias (identificación de palabras y recuentos) a como máximo M tokens.
Con estas condiciones, es posible construir un flujo de entrada donde el token T nunca será detectado si el N es lo suficientemente grande como para que el flujo contenga diferentes tokens M entre T's.
Esto es independiente de los detalles del algoritmo top-N. Solo depende del límite M.
Para ver por qué esto es cierto, considere el flujo entrante formado por grupos de dos tokens idénticos:
donde las a y las b son tokens válidos que no son iguales a T.
Observe que en esta secuencia, la T aparece dos veces para cada ai y bi. Sin embargo, rara vez parece que se elimine del sistema.
Comenzando con una memoria vacía, el primer token (T) ocupará un espacio en la memoria (delimitado por M). Entonces a1 consumirá una ranura, hasta a- (M-1) cuando se agote la M.
Cuando llega aM, el algoritmo tiene que eliminar un símbolo, así que sea la T. El siguiente símbolo será b-1, lo que provocará que a-1 se elimine, etc.
Por lo tanto, el T no permanecerá residente en la memoria el tiempo suficiente para generar un conteo real. En resumen, cualquier algoritmo perderá un token de frecuencia local suficientemente baja pero frecuencia global alta (a lo largo de la transmisión).
fuente